Ohm's law is one of the fundamental laws of physics and electrical engineering. It was formulated by German physicist Georg Simon Ohm in 1827 and describes the relationship between electric current, voltage, and resistance in an electrical circuit.
In this article we will discuss the definition, explain the formula and explain the fundamental characteristics and concepts related to this law.
Definition of Ohm's law
Ohm's law is a law in electricity that states that: “the strength of a direct current is directly proportional to the potential difference and inversely proportional to the resistance of the circuit.”
Ohm's law formula
In mathematical terms, Ohm's law is applied by the equation:
Where:
-
R is the electrical resistance. By resistance we mean the obstacle that the current finds in its path; the higher it is, the more difficult it will be for the current to pass through it. The unit of measurement for resistance is ohms, symbolized by the Greek letter omega (Ω).
-
I is the intensity of an electric current that passes through a conductor expressed in Amps (A).
-
V is the voltage. By voltage, however, we refer to the potential difference between one point and another, expressed in Volts (V).
The current intensity of electrical charges is directly proportional to the applied voltage and inversely proportional to the resistance.
For voltage, however, the higher it is, the greater the force of attraction it generates to move the charges, so for the same resistive value it will be directly proportional to the current.
What is Ohm's law triangle?
Ohm's law triangle is a trick to remember the formula.
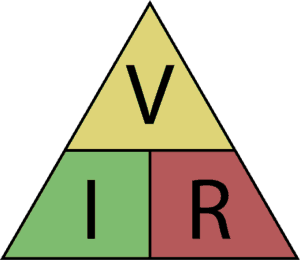
To obtain the triangle formula we have to cover the variable we want to obtain with our hand. If the two remaining elements are on top of each other they are divided, if they are in a line they are multiplied.
The three possible combinations are:
-
I = V / R
-
V = I · R
-
R= V / I
Key components of Ohm's law
To fully understand Ohm's law, it is essential to analyze the three main components involved: voltage, current, and resistance.
Voltage
Voltage, also known as potential difference or strain, is the force that drives electrons to move through a conductor. It is a measure of the electrical potential energy per unit charge.
When there is a potential difference between two points in a circuit, electrons flow from the point of higher potential to the point of lower potential. This flow of electrons is what we call electric current.
Voltage is measured in volts (V), and one way to visualize it is to think of a hydraulic system. If we consider water in a pipe, the voltage would be equivalent to the pressure pushing the water through the pipe. The higher the pressure, the greater the flow of water.
Endurance
Resistance is a measure of the opposition to current flow in a conductor. It is measured in ohms (Ω), and its value depends on the material, shape, and temperature of the conductor. Conductors with high resistance make it difficult for current to flow, while conductors with low resistance allow current to flow easily.
Resistance is influenced by factors such as the length and cross-sectional area of the conductor. According to the law of resistance of materials, resistance is directly proportional to the length of the conductor and inversely proportional to its cross-sectional area. Conductive materials such as copper and aluminum have low resistance, while non-conductive materials such as wood and plastic have high resistance.
Electric current
Electric current is the flow of electrons through a conductor. It is measured in amperes (A), and can be compared to the amount of water flowing through a pipe. In an electrical circuit, current is the net flow of charge through a cross-sectional area of the conductor per unit time.
There are two main types of current: direct current (DC) and alternating current (AC). In direct current, electrons flow in a constant direction, while in alternating current, electrons change direction periodically.
Ohm's law applies to both types of current, but in alternating current systems, factors such as impedance (a combination of resistance, capacitance and inductance) also play an important role.
Ohm's law explained with an example
To better understand Ohm's law we will resort to a simple hydraulic example:
Imagine a hose connected to the tank of a fire truck.
-
Voltage (V). Voltage is the power of the truck’s water pump. The water pump “applies a voltage” to the circuit.
-
Resistance (R). The resistance of the electrical circuit is equivalent to the resistance offered by the hose (diameter). If the hose has a large diameter, the water will flow more easily than if the diameter is small. In the example of the electrical circuit, the concept of resistance is equivalent but is expressed in Ohms (Ω).
-
Current intensity (I). In our example, the intensity is the number of water molecules flowing through a section of hose per unit of time. In an electrical circuit, the equivalent of molecules is electrical charges.
In this simile, it is easy to understand that if we increase the capacity of the pump (voltage) the water flow (intensity) will increase. In the same way, if we use a smaller hose (greater resistance), the flow will also decrease.
Limitations of the law
Although Ohm's Law is extremely useful, it does have some limitations. The main limitation is that it only applies to materials and components that behave linearly, i.e. those that have a linear relationship between voltage and current. These materials are called "ohmic," and their resistance is constant regardless of voltage and current.
However, not all materials behave ohmically. Semiconductors, such as silicon, have a non-linear relationship between voltage and current, meaning their resistance changes with the applied voltage. Devices such as diodes and transistors do not follow Ohm's Law strictly, as their behavior is more complex.
Also, in alternating current (AC) circuits where both capacitance and inductance are present, Ohm's Law must be modified to account for impedance, which is the total opposition to current flow, including resistance, capacitance, and inductance.
Ohm's law and electrical power
Sometimes the formula for electrical power is used by applying Ohm's law.
The power formula is as follows (with unit of watts):
P = V · I, (power = voltage x current)
and its variants: V = P / I and I = P/V,
Both variants can be substituted into the Ohm's law formula. For example, if we start from the formula for calculating voltage and substitute, we have the following formula:
V = ( P / V) · R
Isolating the power we have the following result:
V² · R = P
History of Ohm's law
Ohm's Law was discovered and published by Georg Simon Ohm in his book Die galvanische Kette, mathematisch bearbeitet in 1827. Although his discovery is now widely recognized as a fundamental advance in physics and electrical engineering, it was not received with such enthusiasm in its time.
Many contemporary scientists did not fully understand the significance of his work, and Ohm did not receive the immediate recognition he deserved.
The historical context in which Ohm formulated his law is important to understanding the magnitude of his discovery. In the early 19th century, scientists were beginning to explore the properties of electricity and magnetism, but the fundamentals of these phenomena were not well understood. Early research into electricity was largely focused on electrostatic phenomena (electric charges at rest), and the understanding of electric current (charges in motion) was rudimentary.
Ohm carried out a series of careful experiments using conducting wires and different voltage sources to measure the relationship between the current flowing through the conductors and the applied voltage. From these experiments, he formulated his eponymous law, which described the relationship between these three elements mathematically.
Despite initial resistance from the scientific community, Ohm's work laid the groundwork for the development of electrical theory and had a lasting impact on engineering and technology. In recognition of his contributions, the unit of electrical resistance in the International System of Units (SI) was named in his honor: the ohm (Ω).