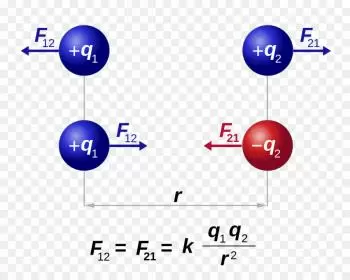
Coulomb's law is a law that defines the force exerted by an electric field on an electric charge. This is the force that acts between electrically charged objects, and is operationally defined by the value of the interaction between two stationary point electric charges in vacuum.
Coulomb's law states: “The electrical force of attraction or repulsion between two charges is inversely proportional to the square of the distance between them.”
This force is called the Coulomb force and was described by In physics, the Coulomb force, described by Charles-Augustin de Coulomb.
Charles-Augustin de Coulomb invented the torsion balance to measure magnetic and electrical attraction. This instrument is capable of measuring the torque resulting from the application of one or more forces on its arms.
Definition of Coulomb's law
Coulomb's law states that the force of interaction between two point electric charges is directly proportional to the product of the magnitudes of the charges and inversely proportional to the square of the distance between them. This force is attractive if the charges are of opposite sign and repulsive if they are of the same sign.
The law describes how electric charges influence each other through space, and is fundamental to electromagnetic theory.
Mathematical formula
The Coulomb force can be calculated using the following equation:
Where:
-
F is the Coulomb force expressed in Newtons (N).
-
q 1 is the first point charge expressed in Coulombs (C).
-
q 2 is the second point charge (C).
-
r is the distance between two point charges expressed in meters (m).
-
k C is an electrostatic constant whose value is approximately 8.988 × 10 9 N m 2 C -2
All variables described in this definition correspond to the international system of units.
If the sign of the force is positive, it means that the force is repulsive. If, on the other hand, it is negative, the force is attractive.
From the formula we can draw several conclusions that the force is directly proportional to the product of the electric charges q 1 and q 2
Examples of Coulomb's law
Coulomb's law applies wherever electric charges and electric fields are involved. Some examples in everyday life are:
- Electromagnets : An electromagnet generates a magnetic force when an electric current flows through a wire wound around a ferromagnetic core. The interaction between the moving electric charges within the conductor and the resulting magnetic field follows the principles of Coulomb's law, as the charges within the conductor attract or repel each other depending on their signs and the relative distance between them.
Electric Motors : In electric motors, the force that drives motion comes from the interaction between electrical charges within magnetic fields. This interaction can be understood through Coulomb's law, as charges within the motor coils interact with other charges in the rotor and stator, generating torque that causes motion.- Electrostatic charges on a balloon : If we rub a balloon against a woollen jumper, some electrons are transferred from the jumper to the balloon, charging it negatively. This build-up of charge causes the balloon to exert an attractive force on oppositely charged objects, such as the atoms in the ceiling. Due to Coulomb's law, the excess electrons in the balloon generate an attraction towards the protons of the atoms in the ceiling, allowing the balloon to temporarily stick to the surface. This phenomenon is an example of how electrostatic forces act in the macroscopic world.
- Electric sparks : On a dry day, when a person walks on a carpet and then touches a metal surface, he or she may experience a small electric shock. This happens because, when walking, charges of different signs accumulate on clothing or on the body, creating an imbalance. Coulomb's law explains the accumulation of charges and the subsequent release of energy in the form of a spark when the electrical balance between the body and the metal object is restored.
- Lightning : During a thunderstorm, charges of different signs accumulate in the clouds. When the difference in charge is large enough, an electric discharge occurs in the form of lightning. This phenomenon is a manifestation of Coulomb's law, since opposite charges between the cloud and the ground attract each other with great force.
- Electrostatic charge on clothing : When we rub a wool or synthetic sweater against our clothing, electrons are transferred, creating an electrostatic charge. This sometimes causes clothing to stick to our skin or small sparks to appear when we touch a metal handle. This happens because the electrical charges are interacting according to Coulomb's law.
- Interaction between dust particles and charged surfaces : In dry places or when we rub certain materials, there can be a build-up of static charges. This causes small dust particles to stick to charged surfaces, such as a phone screen or a TV screen, showing how opposite charges attract charged particles.
- Home Appliances and Touch Screens : Electronic devices such as mobile phones and touch screens work through the interaction of electrical charges. For example, when you touch a capacitive screen, electrons from your finger interact with the device's sensors, generating a response on the screen, all governed by Coulomb's law.
Exercise on the application of Coulomb's law
Determine the electric force between two charged spheres of 1 μC each, placed at a distance of 1.0 cm.
Performing the exercise
Two point electric charges are placed at a distance of 1 cm from each other.
We want to determine the electrical force established between the two electrical charges, knowing that each charge has an intensity equal to 1 μC.
We apply Coulomb's law directly:
In which:
Q 1 = Q 2 = Q = 1 μC = 10 -6 C.
r = 1.0 cm = 10 -2 m
Replacing the formula we have:
F= 8.988 · 10 9 · (10 -6 · 10 -6 ) / 10 -2 = 89.88 N