Ampère's Law is one of the fundamental principles of electrodynamics that governs the behavior of magnetic fields generated by electric currents. Formulated by André-Marie Ampère in the 19th century, this law has been fundamental in the understanding and development of electromagnetic theory.
This law is related to the interaction between electric currents and magnetic fields. Additionally, it is one of the four fundamental equations of electromagnetism, which also include Maxwell's equations, and provides a solid foundation for understanding the behavior of magnetic fields.
What does Ampère's law establish?
Ampère's law states:
- The circulation of the magnetic field of constant currents throughout any closed circuit is proportional to the sum of the forces of the currents that cross the surface of the circuit.
- If direct current is used, the magnetic field is continuous.
- If alternating current is used, the magnetic field is alternating.
Ampere's law formula
Ampère's law can be represented with the following equation:
In this formula for calculating the magnetic field, the integral represents the circulation of field lines along a closed path, and:
-
μ 0 is the vacuum permeability
-
dl is a vector tangent to the path chosen at each point
-
I T is the net current intensity that crosses the surface delimited by the path, and will be positive or negative depending on the direction in which it crosses the surface.
Examples of Ampère's law
Example 1: The electromagnet
An electromagnet is a type of magnet that is activated when an electric current flows through it. Usually, electromagnets are made up of a large number of turns of wire very close to each other.
If the ends of this wire are connected to a potential difference, electric current circulates through it and a magnetic field is generated.
This magnetic field is equivalent to the sum of the magnetic fields of each loop and can be calculated by applying Ampère's law.
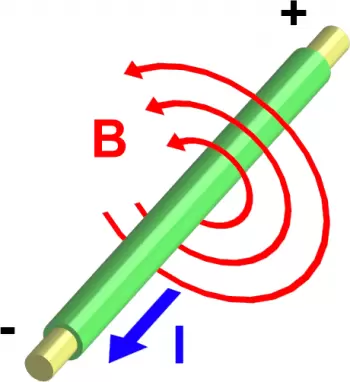
Example 2: Right Hand Rule
Let's imagine a long, straight wire carrying an electric current I.
We can apply Ampère's Law to determine the magnetic field generated by this current.
If we draw a circular path around the wire, the circulation of the magnetic field along this path will be proportional to the current passing through the area enclosed by the path.
This is known as the right-hand rule and is used to determine the direction of the magnetic field around the conductor.
Uses and applications
- Calculation of magnetic fields : this law is a fundamental tool for calculating magnetic fields generated by electric currents. This is essential in the construction of electromagnets, electric motors and transformers, where the generated magnetic field is controlled and used.
- Electromagnetic theory : as we mentioned above, it is one of Maxwell's equations that, together with the other three equations, completely describes electromagnetism. These equations are fundamental in the theory of electromagnetic fields and have given rise to many technological applications, such as radio, television, and wireless communication.
- Electromagnetic induction : Ampère's law is essential to understanding electromagnetic induction, the principle on which electrical generators and the generation of electricity in power plants are based. This law allows us to calculate the electromotive force induced in a circuit due to changes in the magnetic field flow.
- Magnetic circuit design : In electrical engineering, it is used to design efficient magnetic circuits, such as transformer cores and coils. This ensures that energy is transferred effectively and losses are minimized.
Force of attraction between conductors with electric current
Two drivers influence each other. Parallel and rectified electric currents attract, parallel and opposite currents repel.
This can be understood in terms of the Lorentz force: current in one wire generates a magnetic field which, due to Lorentz's law, produces a force on moving charges in the other wire and therefore both wires. They feel a mutual strength.
Ampère's law and Maxwell's laws
After the discovery of Ampère's law, Maxwell summarized the entire theory of electromagnetism in four equations: Maxwell's laws.
Ampere's law, with an extension for time-dependent dielectric displacement, is one of them. However, Maxwell's laws are often written in differential form, that is, not with integrals as before, but equations that give relations between the derivatives of the electric and magnetic fields.