The triangle, a geometric figure composed of three segments that connect three different non-aligned vertices, represents one of the fundamental polygonal shapes in geometry. Its relevance in science and technology dates back to ancient times, since it is one of the most essential and widely used geometric figures.
A significant feature of triangles is their invariability, making them crucial elements in architectural design, such as the Eiffel Tower, based on a composition of triangular shapes, and engineering, including fixed structures for solar panels. In addition, they play a fundamental role in geometry, since all polygons can be decomposed into triangles.
Characteristics of triangles
Triangles are fundamental geometric figures with various characteristics that define their structure and properties. Here are some of the most important features of triangles:
- Three sides : Triangles are polygons that have exactly three sides. These sides are line segments that connect three points called vertices.
- Three angles : Each triangle consists of three interior angles at its vertices.
- Sum of angles : In a triangle, the sum of the interior angles is equal to 180 degrees. This is valid for any type of triangle, whether equilateral, isosceles or scalene.
- Corresponding sides and angles : In a triangle, the corresponding sides and angles are equal in congruent triangles. Congruence refers to the equality of shape and size.
- Height and median : In a triangle, the height is a line segment perpendicular to one side and passing through the opposite vertex. The median is a segment that connects a vertex to the midpoint of the opposite side.
Types of triangles
These geometric figures can be classified according to different criteria:
Due to the size of the interior angles it can be:
- Acute triangle : all interior angles are acute (less than 90 degrees).
- Obtuse triangle : there is an angle greater than 90 degrees.
- Right triangle – One of the angles is 90 degrees, a right angle. In this case, the two sides that form a right angle are called legs and the side opposite the right angle is called the hypotenuse.
As in Euclidean geometry the sum of the angles of a triangle is 180º. Therefore, at least two angles in the triangle must be acute (less than 90º).
Due to the number of equal sides these figures can be:
- Scalene triangle : the three sides are not equal.
- Isosceles triangle s: two sides are equal. These sides are called side, the third side is called base. In an isosceles triangle, the angles at the base are equal.
- Equilateral triangle : all three sides are equal. In an equilateral triangle, all angles are equal to 60°.
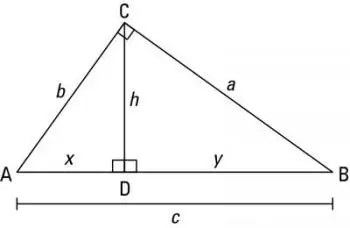
Calculate the area and perimeter of a triangle
Based on the figure at the bottom, to obtain the perimeter and area of a triangle, we can use the following formulas:
Perimeter
To calculate the perimeter we simply have to add the lengths of the sides of the figure: a + b + c.
Area
The formula to find the area of a triangle is half the product of the base (not the sides) and the height:
A = (b h) / 2
In the event that we do not know the height, we can apply Heron's formula.
Where:
-
a, b and c correspond to the three sides of the geometric figure.
-
A is the area
-
s is the semiperimeter (find the perimeter and divide by two):
In the case of a right triangle, one of the legs is the base and the other corresponds to the height. This way it is easier to calculate the area.
Properties and theorems
Pythagoras theorem
The Pythagorean theorem is one of the most famous and useful geometric results. It applies to right triangles, those with a right angle (90 degrees). The theorem states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides. Mathematically, it is expressed as:
a² + b² = c²
Where "a" and "b" are the lengths of the legs and "c" is the length of the hypotenuse.
The Pythagorean theorem is fundamental in geometry and trigonometry and is applied to a wide variety of problems, from calculating distances on maps to solving quadratic equations.
Bisector Theorem
The Bisector theorem refers to the bisector of an angle in a triangle. It states that the bisector of an angle divides the side opposite the angle into two segments that are proportional to the other two sides of the triangle. Mathematically, it is expressed as:
a/d = b/e
Where "a" and "b" are the lengths of the sides of the triangle, and "d" and "e" are the lengths of the segments into which the bisector divides the opposite side.
This theorem is useful for calculating segments in triangles and finding points of intersection at bisector angles.
Thales Theorem
Thales' theorem is a powerful tool for relating segments in similar triangles. It states that if a parallel line cuts two sides of a triangle, it divides these sides into proportional segments. Mathematically, it is expressed as:
m/n = p/q
Where "m" and "n" are the lengths of the segments on one side of the triangle, and "p" and "q" are the lengths of the corresponding segments on the other side.
Thales' theorem is fundamental in solving geometric problems and in demonstrating the properties of similar triangles.