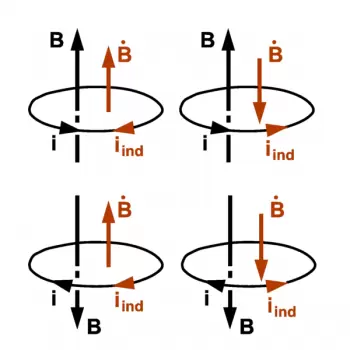
Lenz's law states that when generating an electromotive force (emf) caused by a change in magnetic flux, according to Faraday's law, the induced emf polarity generates a magnetic field that opposes the variation it produces.
This law is based on the Faraday law of induction, also known as the law of electromagnetic induction. In this law, Michael Faraday stated that when a variable magnetic field is connected to a coil, an electromotive force (induced voltage) is induced in it. In other words: the magnitude of the electromotive force induced in the circuit is proportional to the rate of change of the magnetic field.
The law is a consequence of the law of conservation of energy (energy cannot be created or destroyed) and Newton's third law (there is always an equal and opposite reaction to every action).
At first, this might seem to violate the law of conservation of momentum. Still, such an interaction conserves momentum if we consider the rate of electromagnetic fields.
Lenz's law is named after the work done by the physicist Emil Lenz in 1834.
What is the significance of Lenz law?
The Lenz law is important to determine the direction of the emf or induced current without requiring any calculations. Therefore, it is essential in electrical devices that work with a magneto, such as electrical motors, generators, or transformers.
This law defines the changes that occur in the electric field due to a conductor that has the property of varying the magnetic flux. It studies the magnetic flux that is generated inside a conductor due to the action of a changing magnetic field produced by a circulating current.
Lenz's law formula
The flux generated by a uniform magnetic field when passing through a flat circuit can be calculated with the following formula:
Φ = B · S · cos (α)
where
-
Φ is the magnetic flux expressed in Wb.
-
B is the magnetic induction expressed in T.
-
S is the flat surface of the conductor.
-
α is the angle formed by the field's direction and the conductor's surface.
We can use the hand rule to determine the direction of each vector: If the thumb, index finger, and middle finger of the right hand are placed at right angles to each other, with the thumb pointing in the direction the conductor is moving and the index finger pointing in the direction of the field, the middle finger will indicate in the conventional direction of the induced current.
According to the formula, a negative sign indicates that the emf induced in the conductor is in such a direction that it opposes the change in magnetic flux linked with the coil.
Lenz's law applications
-
This law indicates that the change in flow and the induced voltage have opposite signs. With the Faraday law, we can make a physical interpretation of the choice of the sign.
-
Electric generators and motors: When a current is induced in an electric generator, the direction of this induced current is such that it opposes and causes the generator to rotate. It means that the generator needs more mechanical energy in the case of engines. In the case of electric motors, the same thing happens but in the opposite direction.
-
In induction plates and electromagnetic brakes.
-
To understand the concept of magnetic energy storage in an inductor: When connecting an emf through a coil, it generates an electric current, and a back emf appears that opposes the cause that produces it. Therefore, the external source must work to overcome the elements opposing the flow variation. This work can be done by the emf that is stored in the inductor.
-
Current transformers: The most significant use that Lenz's law has in everyday life applications are transformers.
Lenz law examples
The following examples will explain in two particular cases how Lenz law works:
Example 1: Magnet getting closer to a loop
It leads us to conclude that the person pushing the magnet into the loop must exert an opposing force to the repulsive magnetic force to bring the magnet closer to the loop. Then, we would end up with an endless positive feedback loop, breaking the conservation of energy.
The helpful work performed by the force exerted by the person corresponds to the energy delivered to the system and converted into electrical power, as provided by the Principle of Conservation of Energy.
Example 2: Magnet moving away to a Loop
Note: When the north pole of the magnet moves away from the loop, the induced current opposes the change in flux (in this case, decreases), polarizing the loop so that it attracts the magnet.
Again, the force of the person holding the magnet needs to do work, which corresponds to the energy supplied to the system and is converted into electrical energy. See, in the following figure, the magnetic polarization of the spiral face facing the magnet, when its south pole approaches or moves away from it.
