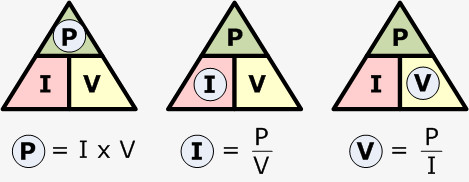
Watt's Law outlines the essential connection between power, current and voltage in an electrical circuit. This standard postulates that the power of a device or circuit is the result of multiplying its voltage by the current that passes through it. In other words, the formula P = VI represents the cornerstone of this relationship.
The electrical consumption of a circuit is intrinsically linked to power. In turn, this power is influenced by the resistance of the device, the input voltage and the current flowing through said resistance.
Watt's law formula
The formula for Watt's law is presented as follows:
P = V · I
Where
-
P is the electrical power of an electrical resistance.
-
V is the voltage applied to the resistance of a circuit.
-
I is the current intensity.
Electrical power consumption is measured in watts (W), voltage in volts (V) and the unit of measurement for intensity is the ampere (A).
In this formula it can be seen that the power consumed is directly proportional to the difference in input and output voltage and intensity.
There are three possible formulas to calculate the electrical power in a circuit.
Creator of Watt's law
Watt's law was not created by James Watt, as the name might suggest. In fact, the law is named after James Watt, the Scottish inventor known for his contribution to the development of the steam engine.
The mathematical formulation of the law is mainly attributed to two scientists: Gustav Kirchhoff and George Simon Ohm. Kirchhoff developed Kirchhoff's laws, which are fundamental in the theory of electrical circuits and which include Watt's Law as a special case.
Ohm, on the other hand, established the basic mathematical relationship between voltage, current and resistance in a circuit, known as Ohm's law.
Relationship to Ohm's law
Watt's law relates power to voltage and current. On the other hand, Ohm's law relates voltage to current intensity and electrical resistance of a circuit.
The formula for Ohm's law is:
V= I·R
Where
-
V is the voltage.
-
I is the current intensity.
-
R is the electrical resistance offered by a circuit measured in ohms.
Since both laws use the same electrical quantities, they are often combined to obtain some useful equations.
Industrial use and applications and in everyday life
Watt's law serves as a fundamental principle in electrical theory, providing an essential understanding of the relationship between electric current, potential difference (voltage), and power in an electrical circuit.
- Electrical Systems Design : By understanding how current, voltage, and power are interrelated, engineers can calculate and plan the power needed to power devices and machinery.
- Energy efficiency : The law is crucial to optimize energy efficiency in electrical devices. It allows devices to be designed and used that operate within specific power ranges, thus contributing to energy conservation.
- Electricity billing : In the domestic and business sphere, Watt's law has a direct impact on the electricity bill. By understanding how the power consumed is calculated, consumers can make informed decisions to reduce consumption and therefore the associated costs.
- Power transmission : In the transmission of electricity over long distances, the formula for calculating electrical power allows engineers to calculate power losses and design efficient transmission systems that minimize these losses, ensuring that the power delivered to the final destination be enough.
- Device optimization : With this law, manufacturers can optimize the performance of electrical devices with more efficient designs and better energy management.
Practical example: charging batteries with a solar panel
Let's say you install a 200 watt (W) solar panel on your roof. Under direct sunlight for 5 hours a day, the panel would generate 1000 watt-hours (Wh) or 1 kilowatt-hour (kWh) daily (200 W × 5 h). Applying Watt's Law (P = IV), if your system operates at 12 volts (V), the current would be approximately 16.67 amperes (I = P/V).
Now, consider charging a battery with a capacity of 500 Wh. Using Watt's Law to calculate charging time, we would have Time (hours) = Energy (Wh) / Power (W), which would result in 0.5 hours or 30 minutes to fully charge the battery (500 Wh / 1000 W).
It is important to take into account the efficiency of the system. Let's assume it is 85%. Applying this efficiency factor to the power generated, the actual power would be 170 W (200 W × 0.85). Adjusting the above calculations, the battery would be fully charged in approximately 1.5 hours (500 Wh / 170 W).
This example illustrates how Watt's law is essential in the design and optimization of solar energy systems to calculate effective power, current, and charging time.