Gauss's theorem for the electric field states that the flux of an electric field through a closed surface (Gaussian surface) is given by the quotient between the total electric charge inside the surface divided by the absolute dielectric constant of the medium (ε 0 ). Any external point load to the surface does not contribute in any way to the total flow.
The Gaussian equation is part of the four Maxwell equations.
The electric field produced by two static charged objects can be obtained by two equivalent procedures: applying Coulomb's law or using Gauss's law. Coulomb's law is a simpler and more direct way of expressing the electric force. On the other hand, Gauss's law is more subtle, more elegant, and sometimes more useful.
Gauss's theorem has a very practical utility. In its physical formulation relating to electric fields, it is ultimately translated into a simple formula, usable by all and with very significant practical implications.
The flow of charges that cross the Gaussian surface is proportional to the number of field lines that cross it.
Statement of Gauss's theorem
Here is the statement of Gauss's theorem for the electric field: the flux of an electric field through a closed surface is given by the relationship between the total electric charge within the surface and the absolute dielectric constant of the medium.
Gauss's law formula
Looking at the Gaussian theorem formula for the electric field, we can write
The Gaussian statement provides a quick and easy way to calculate the electric field flux through a closed surface. Simply calculate the algebraic sum of all the charges that are inside the surface and divide by the absolute dielectric constant.
It is important to highlight some aspects:
-
If we think about the vacuum, we can substitute the absolute dielectric constant of the medium ε m for the dielectric constant of the vacuum whose value we know.
-
To calculate the algebraic sum of all internal charges, it is necessary to take into account the signs of the charges, which can be positive or negative charges.
-
The surface can have any shape as long as it is closed.
-
What matters is the total charge within the surface area. If there are other loads located off the surface, they should not be considered for flow calculation purposes.
-
The theorem is valid for any type of electric field, not necessarily uniform in space. The formula is also valid for any load configuration.
Gauss's law example
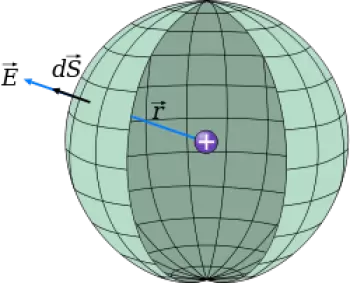
Suppose we want to calculate the electric field produced by a point charge, and let's use Gauss's law to find it.
In our example let us imagine a spherical Gaussian surface of radius r with a charge (q) contained in its center. To calculate the flow integral we will assume that, due to the symmetry of the problem, E must have the radial outward direction of the load (q). This implies that E is parallel to dS at every point on the waiting surface.
Also by the symmetry we must suppose that E depends only on the distance r from the charge q to the considered point, so that E will have the same value for any point on the sphere, and will be constant in the integration.
Under these conditions, the calculation of the flow through the spherical surface will be:
Φ = E (4 · π · r²)
Since the integral is simply the area of the surface of the sphere. Since the total charge contained within our sphere is q, Gauss's law gives us: