The Biot-Savart law is a fundamental law in physics that describes the magnetic field created by a standing electric current. This law provides a way to calculate the magnetic field at a point due to an arbitrary electric current distribution.
It receives its name in honor of the French scientists Jean-Baptiste Biot and Félix Savart, who formulated it in the first half of the 19th century.
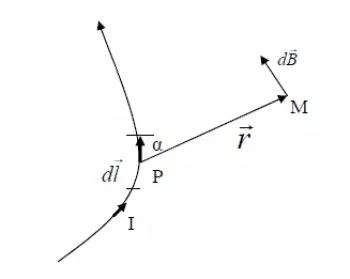
Biot-Savart law formula
The Biot-Savart law states that the magnetic field generated at a point by a small element of electric current is proportional to the magnitude of the current, the length of the conducting element, and the sine of the angle between the direction of the element and the line that joins the element to the point where the field is measured.
Mathematically, it is expressed by the following equation:
Where:
-
B is the resultant magnetic field at a point.
-
μ 0 is the magnetic permeability of the vacuum (μ 0 ≈ 4π×10 −7 T⋅m/A)
-
I is the electric current vector.
-
r is the position vector from the current element to the point where the field is measured.
-
r' is the total displacement vector from the cable element (dl) at the point (l) to the point where the field is calculated (r)
-
dl is a differential element of length along the stream.
The integral in the equation represents the sum of the magnetic effects of all current elements along the conductor.
What is the Biot-Savart law used for?
The Biot-Savart law is a fundamental tool in the study and analysis of electromagnetic phenomena and has a wide range of applications in various fields. Some of the most important applications are the following:
-
Calculation of magnetic fields: this law of electromagnetism allows the calculation of the magnetic field at a specific point generated by a distribution of electric current. This is useful in the design and analysis of electromagnetic devices, such as transformers, electric motors, generators, solenoids, coils, among others.
-
Ampère's Law: The Biot-Savart law is the basis for formulating Ampère's law, which states that the line integral of the magnetic field around a closed path is equal to the magnetic permeability of the medium multiplied by the current enclosed by the path. . The Biot-Savart law provides the mathematical expression needed to calculate the magnetic field in Ampère's law.
-
Magnetic Circuit Design: In the design of magnetic devices and magnetic circuits, it is used to determine the distribution of magnetic fields and magnetic flux through different components such as iron cores, inductors, transformers, and coils.
-
Biophysics: It is also applied in biophysics studies to understand the effect of magnetic fields on biological systems. It is used, for example, in the investigation of the interaction between magnetic fields and biological tissues, such as in nuclear magnetic resonance (NMR) and transcranial magnetic stimulation (TMS).
-
Geophysics: In geophysics, the Biot-Savart law is used in the study of the Earth's magnetic field and in the interpretation of magnetic data collected in geophysical exploration for mineral detection, geological mapping, and prospecting for natural resources.
Biot-Savart law experiment
A classic experiment that illustrates the Biot-Savart law is the magnetic needle experiment. This experiment demonstrates how an electric current generates a magnetic field around it.
Necessary materials
-
A battery or direct current source.
-
A conductor (such as a copper wire).
-
A compass or a magnetic needle.
-
Connection cables.
Procedure
-
Connect the cables to the DC power source and make sure it is turned off.
-
Connect one end of the conductor to a terminal of the current source.
-
Connect the other end of the conductor to the other terminal of the power source.
-
Place the compass or magnetic needle close to the conductor, but not touching it. Make sure the compass is free to move.
-
Turn on the DC power source.
-
Observe the deflection of the magnetic needle as electrical current flows through the conductor.
Explanation
When an electric current is applied to the conductor, a magnetic field is created around the conductor, in accordance with the Biot-Savart law. The compass or magnetic needle, being sensitive to the magnetic field, will deviate from its initial position and point in the direction of the magnetic field generated by the current in the conductor.
The magnitude of the deflection of the magnetic needle will depend on the intensity of the current and the distance between the conductor and the needle.
This experiment demonstrates how an electric current generates a magnetic field and how the direction of the magnetic field is related to the direction of the current in the conductor.
Additionally, it can be used to illustrate other concepts related to electromagnetism, such as the right-hand rule to determine the direction of the magnetic field around a straight conductor.