
A square is a regular geometric shape with four equal sides and four right angles (90 degrees) between those sides.
A square can be classified as a regular polygon, planar and convex quadrilateral. This plane figure is a particular case of the rectangle, rhombus, parallelogram, trapezoid, and kite.
To reconstruct this shape, we only need to know the length of the side or the diagonal.
Squares appear in many geometric solids, but a particular case is a cube. A cube is a platonic solid that all of its faces (six) are made up of squares. The cube is the only Platonic solid that has square faces.
The square is also the basic shape of a platonic mosaic.
What are the properties of a square?
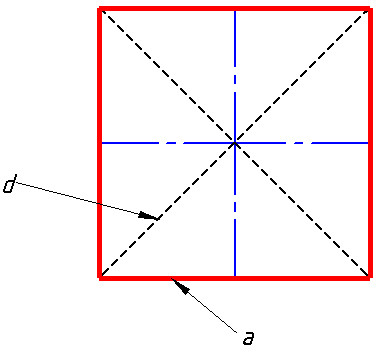
-
All four sides have the same length. Thus, it is a rhombus and an equilateral polygon.
-
The four interior angles are equal, so it is a rectangle and an equiangular polygon. Therefore, interior angles are right angles (measure 90º).
-
The two diagonals of the square are equal, bisect each other, and are orthogonal.
-
The boundary of a square is four times the length of an edge.
-
The point of intersection of the diagonals is the center circumcenter and incircle and the center of symmetry. The square is both a chordal and a tangent quadrilateral.
-
The area of the circumcircle is twice the area of the incircle.
-
It has four axes of symmetry: the two perpendicular bisectors and the diagonals.
-
It is quadruple rotationally symmetric and thus also point symmetric.
-
The symmetry group is the dihedral group D4.
In Euclidean geometry, the square is the particular two-dimensional case of the hypercube and cross polytope.
The notion of a square is generalized in affine plane synthetic geometry by using one of the equivalent statements describing a square in elementary geometry to define the idea. For example, for pre-Euclidean planes, the existence of these figures becomes an additional hypothesis.
In non-Euclidean geometries, squares are generally polygons with four equal sides and equal interior angles.
A square is a polygon in spherical geometry whose sides are great circles intersecting at the same angle. Unlike squares of planar geometry, the angles of a spherical square are more significant than a right angle. Therefore, larger spherical squares have larger angles.
Squares with right angles do not exist in hyperbolic geometry. Instead, squares have angles that are less than a right angle. Larger hyperbolic squares have smaller angles.
Pitagora’s theorem
To find the side length, we can use Pitagora’s theorem.
We must know that according to the Pythagorean Theorem :
-
The hypotenuse of a right triangle is equal to the square root of the sum of the squares of the legs.
-
The leg of a right triangle is equal to the square root of the hypotenuse squared minus the other leg squared.
According to his formula:
d2=a2 + a2
So, a = √(d2 / 2)
Formula to calculate the area of a square
To find the area, we can use the following formula:
Where
-
A is the total area’s shape.
-
a is the length of one side (they are all the same)
-
d is the length of the square’s diagonal from one vertex to the opposite vertex.
How to calculate the perimeter of a square?
The perimeter’s square is the total length of its sides, the length of the boundary. This is the formula to find the perimeter of the shape:
P = 4 · a
Where,
-
P is the perimeter of the geometric figure
-
a is the length of one side of the square.
What other geometric figures can be a square?
The square can also be defined within other geometric figures if they meet some conditions:
-
A rectangle with two adjacent sides of equal length.
-
A rhombus with two adjacent equal angles.
-
A rhombus with a right angle.
-
A parallelogram with two equal adjacent sides and two equal adjacent angles.
-
A parallelogram with two adjacent equal sides and a right angle.
-
A quadrilateral with orthogonal diagonals of equal length bisecting each other.
What does squaring the circle mean?
Squaring the circle is a classic problem in geometry. The task is to construct a square with the same area from a given circle in a finite number of steps. It is equivalent to the so-called rectification of the circle, i.e., the construction of a straight line that corresponds to the circumference of a circle.
What is the magic square?
A magic square of edge length n is a square arrangement of the natural numbers 1, 2, ..., n², in which the sums of the numbers in all rows, columns, and the two diagonals are equal. This sum is called the magic square number.