Thermodynamics, a fundamental branch of physics, unravels the mysteries of heat transfer, and in this broad field, Fourier's law stands as a cornerstone.
This principle, conceived by the illustrious French mathematician and physicist Joseph Fourier in the 19th century, is an essential theoretical pillar for understanding how heat propagates through materials.
This article seeks to delve into the nuances of this law, challenging its inherent complexity with an accessible and understandable approach. From its mathematical foundation to its practical application in everyday situations, we will explore how Fourier's law appears not only in the academic field but also in everyday life, with significant implications.
What is Fourier's law?
Suppose you're holding a hot cup of coffee. Have you ever wondered how heat is transferred from the cup to your hands? The answer lies in Fourier's law.
This law states that the rate of heat transfer through a material is proportional to the temperature gradient. The temperature gradient, in simple terms, is the temperature difference between two points along a material's length.
So, if there's a large temperature difference between the hot coffee and your hands, the heat will transfer more quickly. The greater the temperature difference, the faster the heat will move.
Fourier equation for heat transfer
Now, let's talk about the equation that represents Fourier's law in a more mathematical sense. The formula is:
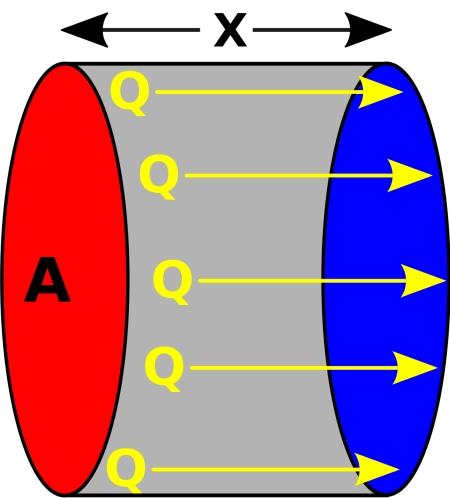
\[ Q = -k A \frac{dT}{dx} \]
Where:
-
\(Q\) is the rate of heat transfer (heat flux).
-
\(k\) is the thermal conductivity of the material.
-
\(A\) is the area through which heat is transferred.
-
\(\frac{dT}{dx}\) is the temperature gradient in the direction of heat flow.
Real example
Now, let's apply Fourier's law to an everyday situation. Imagine you're cooking a delicious soup in a metal pot. The base of the pot is in contact with the hot stove, and you want to know how much heat is transferred to the soup.
First, you need the thermal conductivity of the metal (represented by k ), which is a material-specific property. Next, you measure the contact area between the bottom of the pot and the stove ( A ). Finally, you look at the temperature difference between the hot bottom of the pot and the soup ( dx/dT ).
Using Fourier's law, you can calculate the amount of heat transferred from the stove to the soup.
Applications of Fourier's law
Fourier's law has diverse applications in both engineering and everyday life, as it describes heat transfer in materials. Some of the most relevant applications include:
1. Design of heating and cooling systems
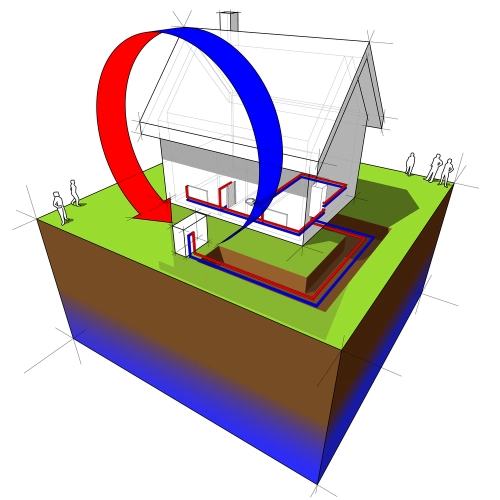Fourier's law is crucial for the design and optimization of thermal systems, such as heating, ventilation, and air conditioning (HVAC) systems.
Engineers use this law to calculate heat flow through walls, windows, and air ducts, helping to create more energy-efficient environments.
2. Thermal insulation
In building construction, Fourier's law is applied to select materials with appropriate thermal properties. Insulation materials such as fiberglass or expanded polystyrene are specifically designed to reduce heat transfer, taking advantage of their low thermal conductivity properties, which helps maintain a stable interior temperature and reduce energy consumption.
3. Materials engineering
In the development and study of new materials, Fourier's law is used to predict how they will behave under heat transfer. This is important in the manufacture of composite materials, semiconductors, and advanced materials used in electronics, aeronautics, and energy.
4. Electronics and electronic devices
Electronic devices generate heat during operation. Fourier's law is used to design heat dissipation systems, such as heat sinks and fans, to prevent electronic components from overheating.
5. Control of thermal processes
In industries such as metallurgy, glass manufacturing, and the chemical industry, Fourier's law is essential for controlling thermal processes. These processes, such as the cooling or heating of materials, are designed taking into account how heat is transferred within the materials.
6. Research on heat transfer in biology
In biology, Fourier's law is used to understand how heat is transferred in living organisms, for example, in the regulation of body temperature in warm-blooded animals and in metabolic processes.
7. Heat transfer calculations in the subsurface
In geothermal energy, Fourier's law is used to model heat transfer through the Earth's layers. This aids in geothermal exploration and in predicting subsurface heat distribution, which is important for geothermal energy extraction.
8. Solar energy technologies
Fourier's law is important in optimizing solar panels and heat transfer in solar thermal systems. It allows us to calculate how heat is distributed and transferred within solar energy collection systems.
9. Thermal simulations in engineering
Thermal simulators, used in mechanical and civil engineering, apply Fourier's law to model heat distribution in complex structures, such as airplanes, cars, buildings, or bridges. These models help predict overheating or energy loss problems.
10. In the food industry
Fourier's law is applied in the engineering of food preservation processes, such as pasteurization or product cooling. It allows the calculation of the rate at which heat is transferred through food during heat treatment, ensuring product safety and quality.
Example in a solar thermal energy installation
In the field of solar thermal energy, Fourier's law plays a fundamental role, as it addresses how heat is transferred through materials, an essential consideration in systems that harness solar radiation to generate thermal energy.
In this section we will analyze the connection between this law of thermodynamics and a solar thermal energy installation:
Solar energy capture
In a solar thermal energy installation, solar collectors are used to capture solar radiation. These collectors are generally composed of specific materials with well-defined thermal conduction properties.
Fourier's law applies here in determining how these materials conduct heat from the collector surface into the circulating heat transfer fluid.
Heat transfer in thermal fluid
The captured solar radiation is converted into heat, raising the temperature of the thermal fluid (such as water or a specialized thermal fluid) that circulates through the solar collectors.
Our law comes into play when analyzing how this heat is transferred along the thermal fluid. The law's equation, considering the fluid's thermal conductivity, transfer area, and temperature gradient, helps us understand and optimize this heat transfer process.
Thermal storage
Many solar thermal energy systems integrate thermal storage devices to accumulate the heat generated during periods of peak solar radiation.
Fourier's law is relevant here when examining how thermal storage materials manage heat transfer during charging and discharging of the system, thus enabling efficient utilization of stored energy.
Heat transfer to the load
Finally, in a solar thermal installation, the stored heat is used to meet heating demands or to produce steam that can drive turbines and generate electricity.
In this process, the Fourier equation is again applied when considering how heat is transferred from the storage system to the load, whether a domestic heating system or a power generation cycle.
Who was Joseph Fourier?
Joseph Fourier (1768–1830) was a French mathematician and physicist whose contributions left a lasting mark on science.
Born in Auxerre, his achievements include the development of the Fourier series, an essential mathematical tool in the analysis of periodic functions. Fourier also played a crucial role in the theory of heat, proposing the famous Fourier law, which describes heat conduction in materials.
His work led him to become a prominent member of the French Academy of Sciences and left a lasting legacy in the study of differential equations and heat transfer.