
Entropy in physics and chemistry is the magnitude that indicates the energy that cannot perform practical work in a thermodynamic process. In general, the total entropy of the universe tends to increase. Consequently, the entropy, that is, the increase in entropy, therefore, the positive variation of this magnitude indicates the natural sense in which an event occurs in an isolated system.
Entropy (S) is a thermodynamic magnitude initially defined as a criterion to predict the evolution of thermodynamic systems. In any irreversible process, the system's disorder increases, and therefore the entropy increases. In reversible processes, the entropy change is zero.
The entropy of a system is an extensive state function. The value of this physical magnitude, in a closed system, is the measure of disorder that a process generates naturally. The concept of entropy describes how irreversible a thermodynamic system is.
In the none reversible process, part of the energy turns into entropy because of the conservation of energy.
What is the unit of entropy?
The units of entropy in the International System are the joules/kelvin (J/K) or Clausius.
We define this SI unit as the change in entropy experienced by a system when it absorbs the thermal energy of 1 Joule (unit) at a temperature of 1 Kelvin.
What is standard entropy?
The standard entropy of a chemical compound is its entropy under the thermodynamic state of 1 atm of pressure. These values are expressed in an entropy table usually indicated at a temperature of 298 K.
Usually, in these tables, the enthalpies of formation of the chemical elements in their standard states set to zero are also expressed. The enthalpy of formation is the amount of energy required to form these compositions.
Entropy formula in physics
In physics, entropy is the thermodynamic magnitude that allows calculating the part of heat energy that cannot be used to produce work if the process is reversible. Physical entropy, in its classical form, is defined by the equation proposed by Rudolf Clausius:
dS=dQ / T
Where:
-
dS is the variation of the entropy.
-
dQ is the variation of energy.
-
T is the temperature.
or more simply, if the temperature is kept constant in the process 1 → 2 (isothermal process):
Thus, if a hot body at temperature T1 loses an amount of heat Q1, its entropy decreases in Q1 / T1. If it transfers this heat to a cold body at temperature T2 (lower than T1), the entropy of the cold body increases more than the entropy of the hot body has decreased because
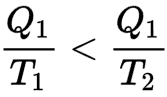
A reversible engine can therefore transform part of this heat energy into work.
In statistical mechanics, the Boltzmann equation is a probability equation relating the entropy S of an ideal gas to the quantity W, the number of real microstates corresponding to the gas macrostate:
S = kB ln W
where kB is Boltzmann's constant (also written simply k) and equal to 1.38065×10 −23 J/K.
Performance of a reversible heat engine
The performance of the reversible machine indicates the maximum ratio of energy that can be converted into work. The following formula can express this relationship:
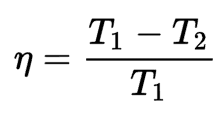
For all the heat energy to be transformed into work, it would be necessary for either the hot spot to be at an infinite temperature or for the cold spot to be at zero kelvin; otherwise, the thermodynamic efficiency of the reversible engine is less than 1.
Why is it not possible to know the absolute entropy?
It is impossible to determine the absolute entropy in the real world because it would require reaching the temperature of zero kelvin.
In physics, we always work on entropy variations because to know the absolute value, it would first be necessary to reach absolute 0. To get to absolute 0, the system would need to cool down to zero kelvin so that the molecules no longer move. From here, increasing the temperature would increase the entropy.
However, from a physical point of view, it is impossible to reach the temperature of zero kelvin, according to the Walther Nernst theorem presented in the third law of thermodynamics.