In geometry, solid shapes constitute an essential category of three-dimensional shapes that occupy space in three dimensions: height, width and length. These solids, defined by faces, edges and vertices, play a fundamental role in the conceptualization and understanding of three-dimensional structures.
The importance of these three-dimensional geometric figures lies in their ability to describe real and abstract objects in space, being crucial in fields such as architecture, design and engineering.
A classic example is the cube, with its six square faces and connected vertices, which represents an elementary geometric solid. The diversity of solid shapes, from pyramids to cylinders, allows us to model and understand the richness of shapes that we find in the three-dimensional world that surrounds us.
What is a solid shape?
A solid shape is a three-dimensional entity that occupies space in the dimensions of height, width and depth. Differentiating themselves from two-dimensional figures, these three-dimensional solids have faces, edges and vertices that define their structure. Geometric bodies encompass various shapes, from prisms and pyramids to spheres and cylinders, each with unique properties.
Flat faces, sharp edges, and connected vertices contribute to the characterization of these solids in three-dimensional space.
In addition to their importance in geometry and mathematics, solid shapes are used in practical applications in architecture, design, and science, serving as essential tools for conceptualizing and modeling objects in the three-dimensional world.
Polyhedra: a particular case
Polyhedra are a particular case of solid shapes whose faces are all polygons. Among them, we can distinguish regular polyhedra and irregular polyhedra.
In three-dimensional geometry, a polyhedron is the equivalent of any polygon in two-dimensional geometry.
Regular polyhedra are made up of regular polygons. These solid shapes can be classified according to the number of faces.
Regular polyhedra are the most symmetrical. There are a total of nine regular polyhedra: five convex polyhedra and four star polyhedra .
A convex polyhedron is a polyhedron that materializes a convex solid, that is, for each pair of points in the solid, the linear segment that joins them is completely contained in the solid.
The five convex examples have been known since ancient times and are called Platonic polyhedra. These are the triangular pyramid or tetrahedron, the cube, the octahedron, the dodecahedron and the icosahedron.
pyramid trunk
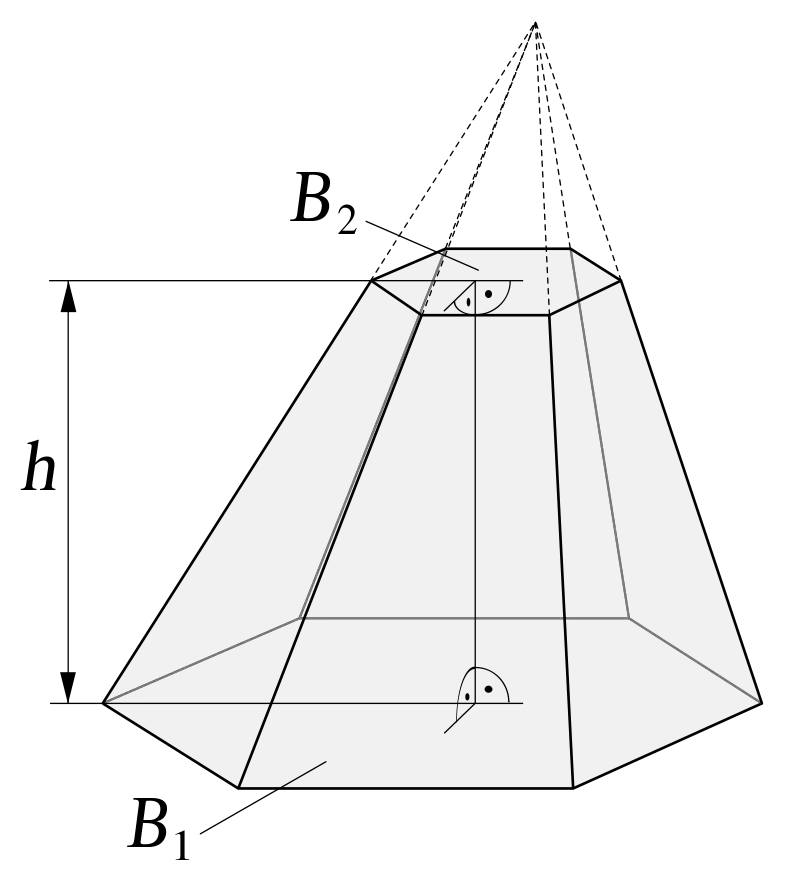The frustum of a pyramid is a type of polyhedron composed of two parallel bases with the same number of edges. On the other hand, it is composed of lateral faces in the shape of a trapezoid. The number of faces is the same as the number of edges of the bases.
This polyhedron is obtained by sectioning a pyramid with an intermediate plane parallel to its base. Of the two resulting pieces, the lower part is a truncated pyramid and the upper part remains a pyramid.
Prisms
A prism is a polyhedron, two of its faces are equal and lie in parallel planes. The remaining faces of the prism are parallelograms that have common sides with these polygons. These parallelograms are called lateral faces of the prism, and the two remaining polygons are called bases.
The polygon found at the base determines the name of the prism, for example: if the bases are triangles it is a triangular prism.
According to the base, the prism can be named as:
- Triangular prism: each base is shaped like a triangle.
- Quadrangular prism: each of the bases is in the shape of a quadrilateral.
- Pentagonal prism: each of the bases is in the shape of a pentagon.
- Hexagon prism: each base is in the shape of a hexagon.
- Octagonal prism: each base has the shape of an octagon.
Rounded solid shapes
We define rounded solid shapes as solid shapes that have at least one curved face. This type of shape is also known as revolution shapes because they can be obtained by rotating a geometric figure around an axis.
Some examples of rounded solid shapes are:
- The sphere is the figure generated by rotating a circle through an axis that passes through the center. In this case it has a single curved surface and no edges. Furthermore, all points on the surface are equidistant from the center of the sphere.
- The cone is generated by revolving a right triangle around one of its legs. This figure has a single flat face formed by a circle.
- The cylinder is formed by rotating a rectangle around one of its sides.
everyday examples
- Soccer Ball : Displaying the perfection of a sphere, the soccer ball illustrates the common presence of this geometric shape in everyday objects.
- Planets of the Solar System : The celestial bodies of the Solar System adopt spherical shapes, highlighting the prevalence of the sphere in the configuration of the universe.
- Cardboard box : With its structure that follows the shape of a rectangular prism, known as a cuboid, cardboard boxes are tangible examples of geometric figures in common packaging.
- Pyramids of Egypt : Representing architectural majesty, the pyramids are examples of quadrangular pyramids that have stood the test of time.
These examples illustrate how geometry is intrinsically present in our environment, from everyday objects to historical monuments.
