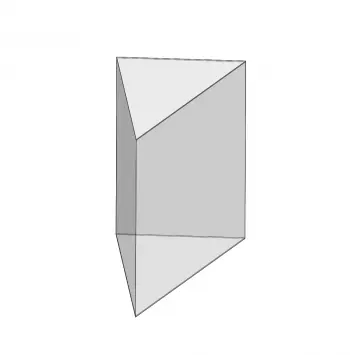
The term "triangular prism" refers to a three-dimensional geometric solid that has a triangular base and side faces that are parallelograms. In other words, it is a prism with a triangle-shaped base.
A triangular prism has three rectangular faces and two triangular faces, making it a specific and distinctive prism. The lateral faces are parallelograms because they have opposite sides that are parallel and congruent.
The height of the triangular prism is the distance between the parallel bases, and can vary in length depending on the size and proportions of the prism.
The triangular prism is just one of the many shapes of prisms that exist, and its specific geometry gives it unique properties and characteristics. It can be used in various applications, such as architecture, geometry or physics, depending on the specific needs and contexts.
Volume of a triangular prism: formula and calculation
The calculation of the volume of a triangular prism is made by multiplying the area of the base by the height of the prism. Here are the three steps to calculate it:
-
Calculate the area of the triangular base: For a triangle, the area is calculated using the triangle area formula, which is (base x height) / 2.
-
Determine the height of the prism: The height of the prism is the perpendicular distance between the two parallel bases.
-
Multiply the area of the base by the height.
Specific formula for the triangular prism:
V = (b t h t / 2) h p
Where:
-
V is the volume of the geometric field.
-
b t is the base of the triangle from one of its bases.
-
h t is the height of the triangle from one of its bases.
-
h p is the height of the prism.
Area of a triangular prism: formula and calculation
To calculate the area of a triangular prism, it is necessary to know the areas of the base and of the rectangles that form the faces of the polyhedron. That is to say:
-
The area of the triangle's base: (base x height) / 2
-
The perimeter of the triangle's base, which is the sum of its three sides.
-
The height of the prism.
Using the triangle area formula, the area of the base can be calculated using the following formula
A = 2 A t + p t h
Where,
-
A is the area of the triangular prism.
-
A t is the area of the base of the prism.
-
p t is the perimeter of the triangular base.
-
h is the height of the prism.
Properties
The main propereties of a triangular prism are the following:
-
Bases: The triangular prism has two bases that are congruent triangles. These bases are parallel to each other and are located at opposite ends of the prism.
-
Lateral Faces: The triangular prism has three rectangular lateral faces. These faces connect the edges of the bases and form parallelograms.
-
Edges: The triangular prism has nine edges in total: three edges that form the triangular bases and six edges that connect the corners of the bases with the corners of the side faces.
-
Angles: Triangular bases have three angles, and each side face has four right angles (90 degrees). Also, adjacent side faces make 90 degree angles to each other.
-
Volume: The volume of a triangular prism is calculated by multiplying the area of the base by the height of the prism. The area of the base is obtained by the formula for the area of a triangle (base x height / 2).
-
Area: The total area of a triangular prism is obtained by adding the area of the two triangular bases and the three rectangular lateral faces.
-
Symmetry: A triangular prism has symmetry about a plane through the center of the prism and parallel to the triangular bases.
Examples
Here are some examples of objects or structures that could be represented as triangular prisms:
-
Tents: Some tents have a structure in the shape of a triangular prism. The bases of the tent are usually triangles and the side faces are rectangular.
-
Signal towers: Some signal towers, such as those used in telecommunications or signal transmission systems, may have a triangular prism shape. The bases would be the support triangles and the lateral faces would be the rectangular panels that house the equipment or antennas.
-
Architectural buildings: Some modern buildings use architectural designs that incorporate triangular prisms into their structure. These prisms can be ornamental elements on the façade or even defined geometric shapes in the main structure of the building.
-
Pools: Some unusually shaped outdoor pools or pools may have a triangular prism shape. In this case, the bases would be the triangular shapes of the pool and the side faces would be the rectangular walls that surround the perimeter.
-
Access ramps: Triangular prisms are sometimes used to create an access ramp that allows people in wheelchairs to overcome the rise of a curb.