Geometry, one of the fundamental branches of mathematics, is responsible for the study of shapes, sizes, relative positions of geometric objects and the properties of space. Within this discipline, one of the key concepts is the bisector.
In simple terms, a bisector is a line, ray, or segment that divides something into two equal or proportional parts.
The term "bisector" comes from the Latin "bisectus," which means "to cut in two." The bisector is used in different geometric contexts to divide angles, segments, arcs and other elements into equal or proportional parts.
Next, we will explore how the bisector is applied in various geometric situations.
Bisector of an angle
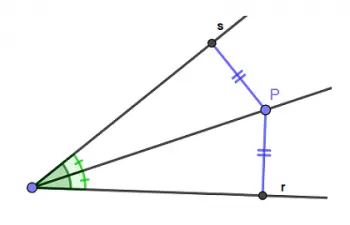
One of the most common applications of the bisector in geometry is the division of angles. The bisector of an angle is a line that divides that angle into two smaller angles that have the same measure.
In other words, divide the angle into two equal parts. This is useful for trisecting angles, constructing specific angles, and solving geometric problems.
The bisector of an angle can be visualized as a line that starts from the vertex of the angle and divides it into two congruent angles.
Bisector of a segment
The bisector can also be applied to line segments. The bisector of a segment divides the segment into two parts of equal length. If we have a segment AB, the bisector will divide it into two segments AC and CB, where AC is equal in length to CB.
This property is especially useful for finding the midpoint of a segment, which has significant implications in analytical geometry and the construction of equidistant geometric figures.
Bisector of an arc
In circular geometry, an arc bisector is a line that cuts the arc exactly in half. This is very useful in geometry problems where precise division of a circle or arc is required.
The bisector of an arc is used, for example, to determine the center of a circle or to divide a circle into two arcs of equal length. This is essential in the construction of circular geometric figures and in solving problems related to circles.
Bisector in triangles
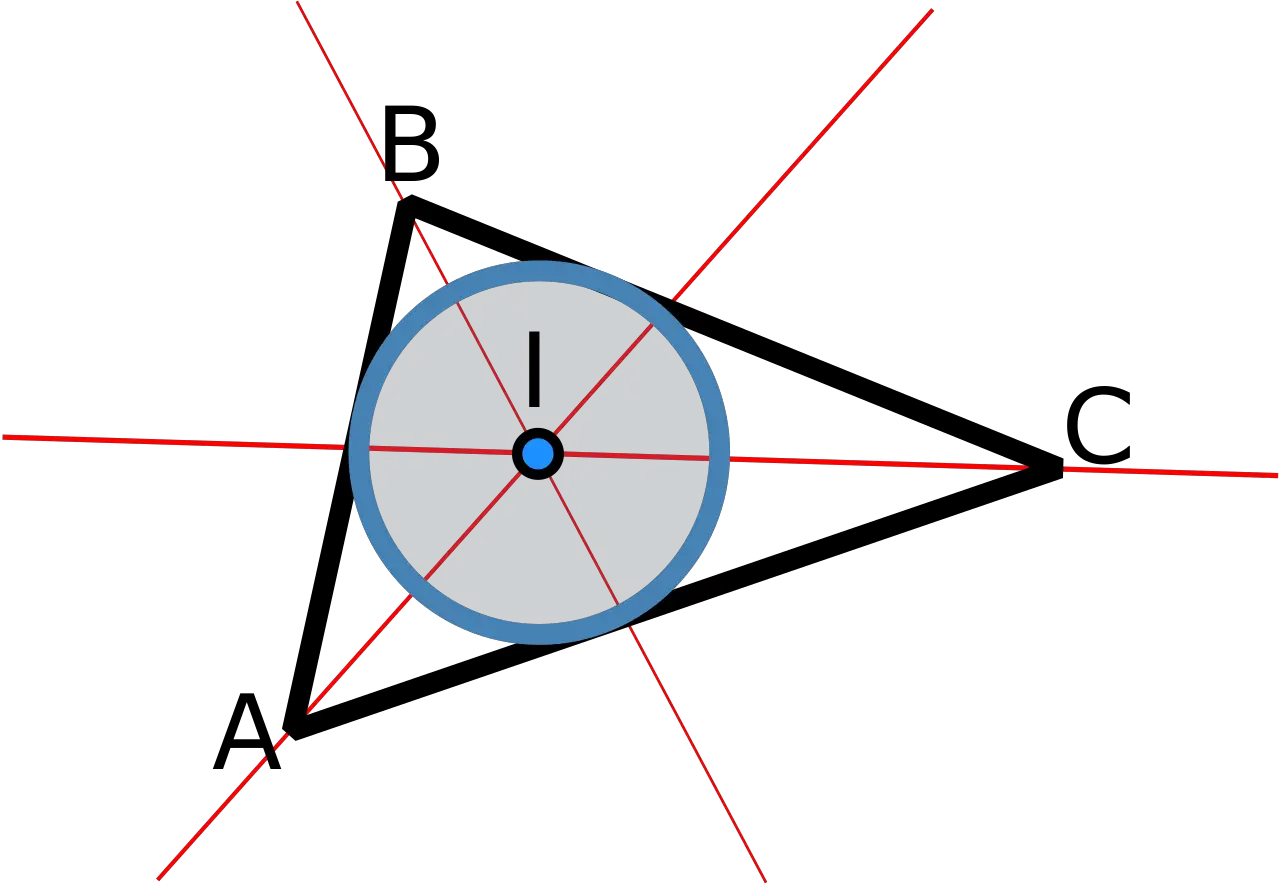This element also plays an important role in the study of triangles.
In a triangle, the bisector of an angle is a line that starts from the vertex of the angle and divides the opposite side into two segments that are proportional to the other two sides of the triangle. This is known as the "bisector theorem" and is useful for solving trigonometry problems and demonstrating properties of triangles.
The theorem states that the ratio between the length of one side of the triangle and the length of the segment that the bisector forms on that side is equal to the ratio between the other two sides of the triangle.
This property is of great importance in solving geometric problems involving triangles and their characteristics.
Applications of the bisector in everyday life
For example, in architecture, it is used to construct precise angles and proportional divisions in building plans and designs. The bisector allows architects and designers to create symmetrical and balanced structures with ease.
In engineering, the bisector is used to determine equidistant points on structures and machines, which is essential to ensure stability and precision in various applications.
Conclusion
The bisector is a fundamental concept in geometry that is used to divide angles, segments, arcs and other elements into equal or proportional parts.
Its application is wide and versatile, playing an essential role in solving geometric problems, constructing geometric figures and demonstrating mathematical properties. Understanding the bisector is essential for those who wish to enter the world of geometry and its application in various disciplines.
From precisely dividing angles in architecture to solving trigonometry problems in mathematics, the bisector is a powerful tool that plays a prominent role in solving problems and creating balanced and symmetrical structures.
