In the realm of geometry, planes serve as fundamental elements. Defined as infinite, flat surfaces extending in all directions, planes aid in comprehending shapes and structures in two dimensions.
In this discourse, we'll elucidate the essence of planes in geometry, detailing their distinctive attributes and multifaceted applications. From crafting geometric figures to troubleshooting and fostering technological innovations, planes play a pivotal role in grasping spatial arrangements and configurations.
What is a plane?
In geometry, a plane denotes an infinite, flat surface extending boundlessly in all directions.
It's akin to envisioning a perpetual sheet of paper, devoid of thickness. There are no discernible boundaries or edges; it's akin to an unbounded realm in two dimensions.
Characteristics of a plane
The quintessential traits delineating a plane in space encompass the following:
- Infinite expansiveness: Foremost among its attributes is its boundless extension in all directions. Regardless of one's distance from any given point on the plane, additional space always prevails.
- Lack of thickness: In contrast to three-dimensional entities like spheres or cubes, a plane possesses no discernible thickness. Visualize gazing upon a drawing upon a sheet of paper; the drawing occupies the plane of the paper, yet the paper itself is so wafer-thin as to be virtually imperceptible.
- Representation through lines: In geometrical contexts, planes are typically represented using lines. These lines, whether straight or curved, stretch limitlessly within the plane, serving as a conduit for depicting relationships between geometric entities.
- Independence from coordinate systems: Planes remain unaffected by the coordinate systems employed for their depiction. Regardless of the configuration of x and y axes, fundamental properties such as infinity and lack of thickness persist unaltered.
- Inclusion of infinite points: Given its infinite expanse, a plane encompasses infinitely many points, each distinct and identifiable via coordinates within a designated coordinate system.
- Absence of preferential direction: Unlike segments or lines, which possess directional attributes, planes lack a discernible orientation. They may be conceptualized as orientation-agnostic surfaces wherein all directions are equally valid.
Types of planes
Within the domain of geometry, several plane typologies serve diverse purposes and applications. Here are some prevalent examples:
- Horizontal: Extending parallel to the Earth's surface, a horizontal plane remains level and uninclined in a three-dimensional context.
- Vertical: In contrast, a vertical plane ascends perpendicularly from the Earth's surface, facilitating the representation of spatial arrangements within a three-dimensional domain.
- Inclined: Neither horizontally nor vertically aligned, an inclined plane assumes an angled orientation, crucial for analyzing forces, gradients, and kinematics in physics and mechanics.
- Cartesian: A two-dimensional coordinate system incorporating perpendicular axes (typically labeled x and y), the Cartesian plane finds widespread utility in mathematical domains, enabling the representation of points, graphs, and functions.
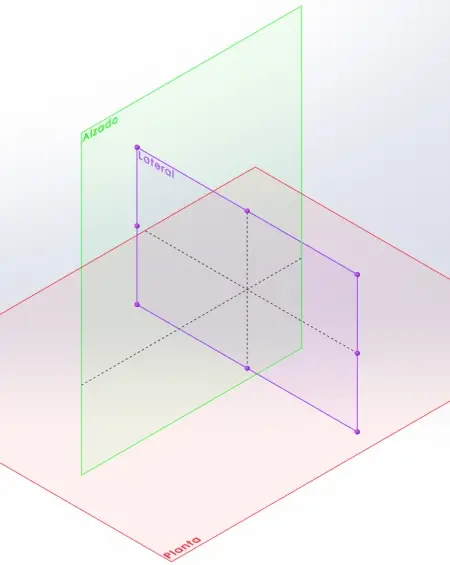
- Projection: In technical illustration and design, projection planes facilitate the portrayal of three-dimensional objects within two dimensions. Projection plans encompass plan, elevation, and profile views, each offering distinct perspectives of an object from varied angles.
- Tangent: Tangent planes, touching a surface at a solitary point, form a perpendicular relationship with the line traversing that point. They feature prominently in calculus and differential geometry, elucidating the interface between curves and surfaces at specific junctures.
- Parallel: Devoid of intersection with a designated plane, parallel planes maintain equidistant trajectories throughout their expanse. They prove invaluable in geometric analyses pertaining to lines and angles in parallel configurations.
- Perpendicular: A perpendicular plane assumes a special status, forming a right angle (90 degrees) concerning another plane or line.
Difference between plane and area
In geometrical parlance, a "plane" signifies a two-dimensional surface extending boundlessly in all directions, akin to a sheet of paper. An abstract construct bereft of thickness, it's defined by the intersection of two lines or a succession of points in space.
Conversely, "area" serves as a quantitative measure of a two-dimensional surface's extent, representing the expanse covered by a figure on the plane and expressed in square units (e.g., square meters or square centimeters).
Whereas a plane constitutes the surface per se, area quantifies the spatial occupancy of said surface.