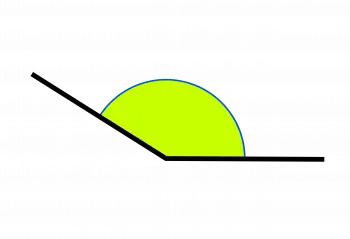
An obtuse angle is a type of angle that measures more than 90 degrees but less than 180 degrees. In other words, it is an angle whose opening is greater than a right angle (which measures exactly 90 degrees) but less than a straight angle (which measures 180 degrees). The term "obtuse" comes from the Latin "obtusus", which means "blunt" or "not sharp".
Visually, an obtuse angle would look like a wider opening than a right angle, but would fall short of a straight line. If an obtuse angle is drawn on a surface, it would look like a "V" open outwards.
Characteristics
Obtuse angles have several distinctive features that set them apart from other types of angles. Here are some of its key features:
-
Measure greater than 90 degrees: An obtuse angle has a measure greater than 90 degrees (π/2 radians) but less than 180 degrees (π radians). In other words, it is larger than a right angle (90 degrees) but smaller than a straight angle (180 degrees).
-
Opposite arms: Obtuse angles are formed by two rays or lines, called arms, that share a common point called the vertex. These arms extend in opposite directions from the apex.
-
They do not form a straight line: Since the measure of an obtuse angle is less than 180 degrees, the arms do not extend in the same direction and therefore the obtuse angles do not form a straight line.
-
Location in a plane: Obtuse angles exist within a plane, which is a two-dimensional surface. In a plane, angles are formed by the intersection of lines or segments.
-
Triangle category: Obtuse angles are also associated with obtuse triangles, which are triangles that have an internal angle greater than 90 degrees. In these triangles, the other two angles are acute (less than 90 degrees).
-
Utility and applications: Obtuse angles and their study are important in mathematics and geometry, since they allow solving problems in design, construction, navigation, engineering, and many other disciplines.
Relationship of obtuse angles with triangles
Obtuse angles are directly related to triangles, specifically in regards to the types of triangles based on the measure of their internal angles.
A triangle is defined by the sum of its three interior angles, and the sum of the interior angles of any triangle always equals 180 degrees (π radians).
When we talk about the measure of the internal angles of a triangle, we can classify the triangles according to the measure of their angles in:
-
Acute Triangle: An acute triangle is one in which all its internal angles measure less than 90 degrees (π/2 radians).
-
Right Triangle: A right triangle is one that has an internal angle of 90 degrees (π/2 radians). In this type of triangle, one of the angles is a right angle.
-
Obtuse triangle: An obtuse triangle is one that has one of its internal angles greater than 90 degrees (π/2 radians) and, therefore, the other two angles are acute.
It is important to note that in any triangle, the sum of the interior angles is always 180 degrees. So if a triangle has one obtuse angle, the other two angles must be acute so that the total sum is 180 degrees.