Geometry is a branch of mathematics that focuses on the study of the shapes, sizes, and properties of geometric objects, such as points, lines, segments, polygons, and circles.
One of the fundamental topics in geometry, and in particular triangles, is the study of angles and segments, and one of the most important theorems related to these concepts is the bisector theorem.
This theorem plays a crucial role in the division of angles and segments, and has applications in various areas of mathematics and physics.
Definition of angles and bisector
Before we dive into the bisector theorem, it's important to understand some key concepts in geometry. An angle is the region formed by two rays that share a common point, called a vertex. Angles are measured in degrees, and a full angle is 360 degrees. In many cases, we need to divide an angle into two equal parts, and that leads us to the notion of a bisector.
An angle bisector is a line, ray, or segment that divides the angle into two congruent angles, that is, two angles that have the same measure. In other words, the bisector cuts the angle in half. In the case of a 90 degree angle, the resulting bisector would have an angle of 45 degrees on each side.
The triangle bisector theorem
The bisector theorem states that, in a triangle, the bisector of an angle divides the opposite side into segments proportional to the other two sides. This may seem like a complex statement, but we can break it down and understand it better through an example.
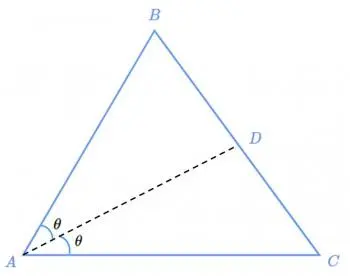
Consider a triangle ABC, where the angle at vertex A is being bisected by a line crossing the opposite side BC at point D. The theorem tells us that the ratio between BD and CD is equal to the ratio between AB and AC.
Mathematically, this can be expressed as follows:
This theorem is especially useful in solving geometry problems involving angles and segments. It can help us find unknown lengths or demonstrate properties of triangles and other geometric figures.
Proof of the bisector theorem
The proof of the bisector theorem involves the use of properties of similar triangles and the application of Thales' theorem. Here is a brief explanation of how it is demonstrated:
-
We start with triangle ABC and its bisector that crosses side BC at point D.
-
We apply Thales' Theorem, which states that if we have two parallel lines cut by transversal lines, proportional segments are created. In this case, we draw a line parallel to sides AC and BD that passes through point C.
-
This gives us two similar triangles: ACD and ABC, where the angles are equal and the lines are parallel, which implies proportional segments.
-
Using the similarity property of triangles, we can state that:
This is the equality we wanted to prove, and thus the proof of the theorem is completed.
Examples of applications of the theorem
The bisector theorem has several applications in geometry and mathematics. Some of the most common application examples include:
- Geometry problem solving: The theorem is used to find unknown lengths or angles in triangles and other geometric figures when certain proportion relationships are known.
- Demonstration of properties of triangles: Used to show that certain triangles are similar or that certain points are on a straight line.
- Geometric Construction: Helps in constructing accurately bisected angles, which is useful in various design and architectural applications.
- Trigonometry studies: The theorem is also applied in trigonometry to solve problems related to sines, cosines and tangents.
- Physics problem solving: Used in physics to understand particle trajectories and the direction of forces in physical systems.