In thermodynamics, an isobaric process is a change in the state of a certain amount of matter in which the pressure remains constant . What does change is one or more of its state variables, such as volume and temperature. If heat is transferred to the system, work is done and the internal energy of the system also changes.
The isobaric process for ideal gases follows Charles's law. According to this law, for a fixed mass of ideal gas at constant pressure, the volume is directly proportional to the temperature in Kelvin.
Isobaric processes are governed by the first law of thermodynamics. In these processes, the increase in enthalpy (ΔH) is equal to the heat transferred to the system, and the work performed is P ΔV. The relationship between internal energy, work and heat is expressed as ΔU=Q−PΔV, where Q=ΔH.
Definition of an isobaric process
An isobaric process is one in which the pressure remains constant while the system undergoes other changes. In more technical terms, the derivative of pressure with respect to time is said to be equal to zero, i.e.:
dP/dt=0
This type of process differs from other thermodynamic processes, such as isochoric processes (in which the volume is constant), isothermal processes (in which the temperature is constant) and adiabatic processes (in which there is no heat transfer).
Even though the pressure remains constant, other properties of the system, such as volume and temperature, can change. As the volume of the system changes, work is done, and this work is related to the change in volume under constant pressure.
Examples of isobaric processes
To better understand this thermodynamic process, it will help us to see a couple of examples.
-
Expansion phase of an engine cylinder.
-
Boiling water in an open container.
-
Warming of a globe by the effects of solar radiation.
Heating the air in a balloon
At the beginning of the morning it has a certain pressure, volume and temperature. As the air inside it heats up, the pressure increases, but it does not vary due to the increase in its volume.
Expansion phase of a heat engine cylinder
The expansion of air in a cylinder with a movable piston to which heat is supplied occurs by an isobaric process.
The volume will increase proportionally to its temperature and the pressure will remain constant. This is in accordance with Charles' law.
Boiling water in an open vessel
An everyday example of an isobaric process occurs when water is boiled in an open container. When heat energy is supplied to the water, it increases in temperature and turns into steam.
The steam obtained has a higher temperature and occupies a larger volume, however, the pressure remains constant. From the beginning, the pressure is equal to atmospheric pressure.
Ideal gas law and isobaric processes
To fully understand isobaric processes, it is helpful to consider the ideal gas equation of state , which establishes a relationship between pressure (P), volume (V), temperature (T), and the amount of gas (n) in moles, according to the equation:
P·V=n·R·T
Where R is the ideal gas constant. In an isobaric process, the pressure P is constant; this implies that under conditions of constant pressure, the volume of an ideal gas is directly proportional to its temperature.
If the temperature of a gas increases in an isobaric process, its volume will also increase proportionally, and if the temperature decreases, the volume will decrease.
This relationship is a form of Charles's law, which is a special case of the ideal gas law for an isobaric process.
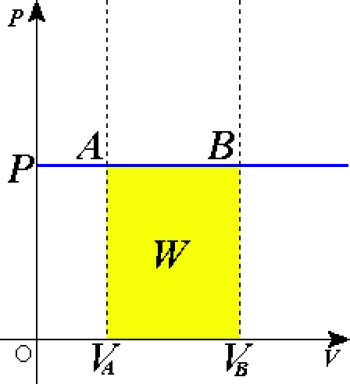
Work performed in an isobaric process
One of the most important aspects of isobaric processes is the work done by or on the system during the process.
In a thermodynamic process, the work done by the system is defined as:
W=∫P·dV
In an isobaric process, where the pressure is constant, this equation simplifies to:
W=P·ΔV
Where ΔV is the change in volume of the system. If the volume increases, the system does work on its surroundings, meaning the gas is expanding. If the volume decreases, the surroundings do work on the system, compressing the gas.
This work performed is closely linked to the change in internal energy and the heat added or removed from the system, according to the second law of thermodynamics, which states:
ΔU=Q−W
Where:
- ΔU is the change in internal energy of the system.
- Q is the heat added to the system.
- W is the work done by the system.
In an isobaric process, heat added to the system not only changes the internal energy of the system, but is also converted to work due to the change in volume. This feature is different from an isochoric process, where all of the heat added is converted to internal energy, since no work is done in a system of constant volume.