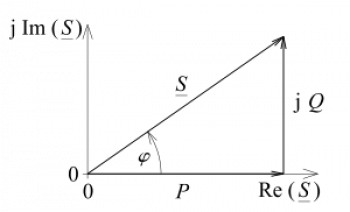
The power triangle, also known as Watt's triangle, is a graphical representation used in electrical theory to analyze the distribution of power in an alternating current (AC) circuit.
It is based on the trigonometric properties of a right triangle, which allows us to calculate and understand the relationship between the three fundamental powers of an electrical system:
- Apparent power (\( S \)) : Represents the total power supplied to the circuit and is measured in volt-amperes (VA). It is the vector combination of active and reactive power.
- Active power (\( P \)) : It is the useful power that is transformed into real work, such as lighting or the movement of motors. It is measured in watts (W).
- Reactive power (Q) : This is the power that does not perform useful work but is necessary for the operation of equipment with inductive elements (such as transformers and motors). It is measured in volt-amperes reactive (VAR).
Power triangle formula
The triangle is made up of three sides, where:
- The hypotenuse represents the apparent power (\( S \)).
- The adjacent leg is the active power (\( P \)), related to the cosine of the phase angle (\( \cos\theta \)).
- The opposite leg is the reactive power (\( Q \)), related to the sine of the phase angle (\(\sin\theta \)).
- Mathematically, the relationship between these powers is expressed by the Pythagorean theorem:
\[ S^2 = P^2 + Q^2 \]
Power factor (PF) is defined as the ratio of active power to apparent power:
\[ FP = \cos\theta = \frac{P}{S} \]
When the power factor is low, it means that there is a high proportion of reactive power, which reduces the efficiency of the electrical system.
Practical examples of the power triangle
Below we show three practical examples
Electric motor with low power factor
An induction motor consumes 10 kW of active power and has a reactive power of 6 kVAR due to its inductive nature.
The apparent power will be:
\[ S = \sqrt{(10^2 + 6^2)} = \sqrt{100 + 36} = \sqrt{136} \approx 11.66 \text{ kVA} \]
Lighting system with power factor correction
A set of LED lamps consumes 5 kW with a reactive power of 1 kVAR.
The apparent power will be:
\[ S = \sqrt{(5^2 + 1^2)} = \sqrt{25 + 1} = \sqrt{26} \approx 5.1 \text{ kVA} \]
Transformer with inductive load
A transformer supplies 50 kW to a system with an inductive load requiring 30 kVAR.
The apparent power of the system will be:
\[ S = \sqrt{(50^2 + 30^2)} = \sqrt{2500 + 900} = \sqrt{3400} \approx 58.3 \text{ kVA} \]
What is the power triangle used for?
The power triangle is a fundamental tool in the analysis and design of electrical systems. Its applications include:
Calculation of electrical power
It allows to determine the power distribution in a circuit:
- The total apparent power (S) supplied.
- Active power (P), which is converted into useful energy.
- Reactive power (Q), which represents the energy exchanged between inductive and capacitive components.
Optimizing circuit performance
By understanding the power distribution, energy losses can be minimized and the power factor improved, thereby reducing unnecessary reactive power consumption and optimizing the use of the electrical grid.
Electrical systems design
It is used for sizing electrical equipment, ensuring that transformers, generators and cables are adequate to handle the required power without overload or excessive losses.
Power factor correction
Many industrial electrical systems require capacitor banks to compensate for reactive power and improve power factor, thereby reducing energy demand from the grid and lowering operating costs.
Failure analysis and preventive maintenance
The power triangle allows for the detection of problems in electrical systems, such as energy losses due to high reactance or load imbalances, helping to prevent failures and optimize maintenance.
Solved exercise on the power triangle
Statement:
An electrical circuit has an apparent power of 800 VA and a power factor of 0.8. Calculate the active and reactive power of the circuit.
Solution:
First, we can calculate the active power (P) of the circuit using the formula P = S x cos(θ), where θ is the phase angle between the current and the voltage. In this case, since the power factor (PF) is equal to 0.8, we know that cos(θ) = PF = 0.8. Therefore, we can calculate the active power as follows:
\[
P = 800 \, VA \times 0.8 = 640 \, W
\]
The active power of the circuit is 640 watts.
Then, we can calculate the reactive power (Q) of the circuit using the formula Q = S x sin(θ). We know that the phase angle (θ) can be calculated from the power factor using the following formula:
\[
\cos(\theta) = \text{FP} \quad \Rightarrow \quad \sin(\theta) = \sqrt{1 - \cos^2(\theta)}
\]
In this case, since FP = 0.8, we can calculate sin(θ) as follows:
\[
\sin(\theta) = \sqrt{1 - 0.8^2} = \sqrt{1 - 0.64} = \sqrt{0.36} = 0.6
\]
Therefore, we can calculate the reactive power as follows:
\[
Q = 800 \, VA \times 0.6 = 480 \, VAR
\]
The reactive power of the circuit is 480 volt-amperes reactive.
Therefore, the active power of the circuit is 640 W and the reactive power is 480 VAR.